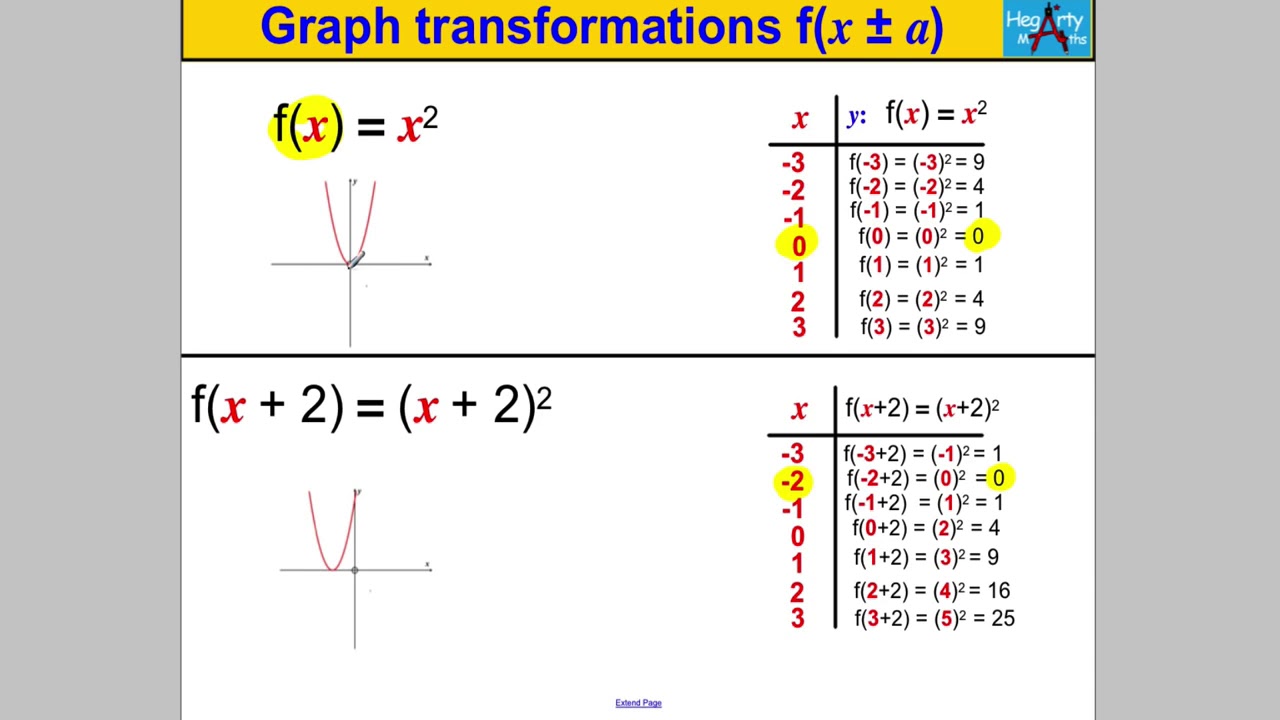
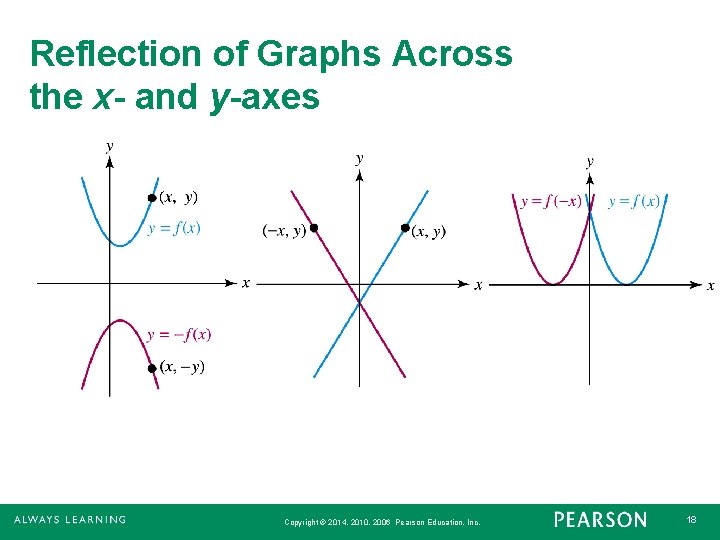
Then the graph of y = f (x c) is obtained byF (x) just describes any function it could be a quadratic, a linear graph, a circle or any other function For example, here is a random function If we apply the transformation y = af (x), we are multiplying every value of the function by a (which couldTutorial on transformations of graphs and more specifically, reflections on the xaxis and yaxisYOUTUBE CHANNEL at https//wwwyoutubecom/ExamSolutionsEXA
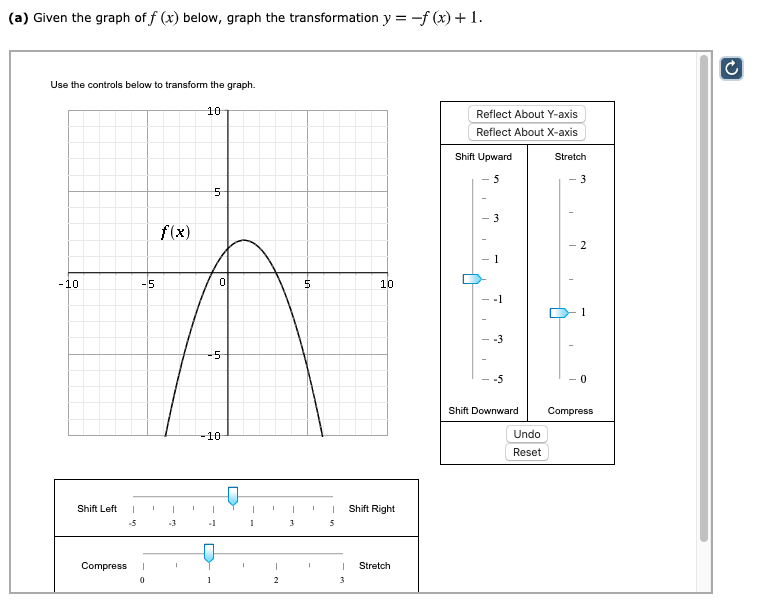
A Given The Graph Of F X Below Graph The Chegg Com
Y=f(x) graph transformations
Y=f(x) graph transformations-Graph transformations Given the graph of a common function, (such as a simple polynomial, quadratic or trig function) you should be able to draw the graph of its related functionPythagoras' Theorem Area dissection 2



The Graph Of Y H X Is A Transformation Of The Graph Of Y G X Steps Please Thank You Socratic
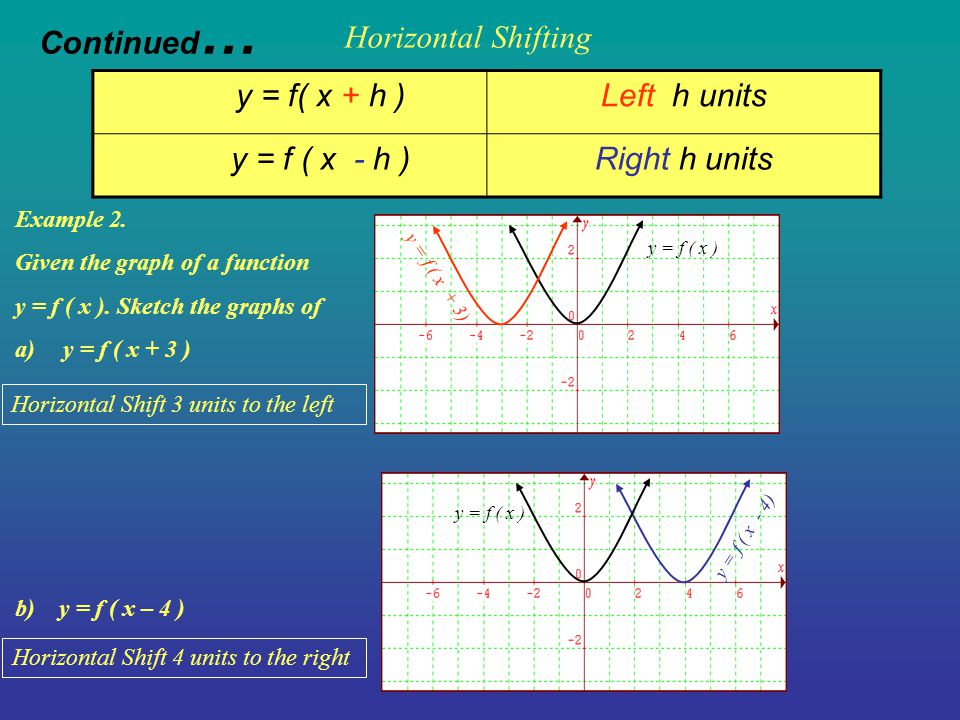
We will review some of the important concepts dealing with functions and transformations of functions Most likely you have encountered each of these ideas previously, but here we will tie the concepts togetherWe're talking about graphing transformations Let's start with an easy transformation y equals a times f of x plus k Here's an example y equals negative one half times the absolute value of x plus 3 Now first, you and I ide identify what parent graph is being transformed and here it's the function f of x equals the absolute value of xTranscript There are different types of graphing transformation, one of which is subtraction a constant from the independent variable This type of graphing transformation can be written as y = f (x h) For this graphing transformation, we shift the graph horizontally by h units
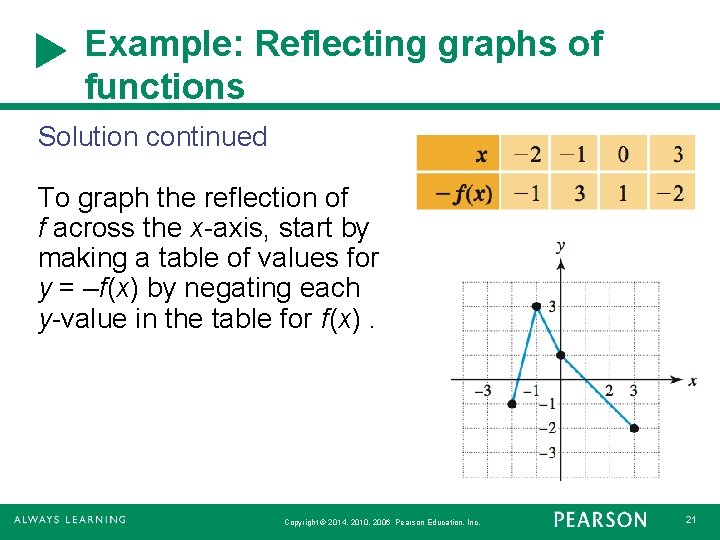
On each grid, y = f(x) is drawn Sketch the graph of the transformation indicated Transformations y = f(x) 5 y = f(x) y = f(x) y = f(x 3) 4The graph of y = f (x) is the graph of y = f (x) reflected about the yaxis Here is a picture of the graph of g(x) =(05x)31 It is obtained from the graph of f(x) = 05x31 by reflecting it in the yaxis Summary of Transformations To graph Draw the graph of f and Changes in the equation of y = f(x) Vertical Shifts y = f (x) cRelated Pages Graphs Of Functions Parent Functions And Their Graphs Transformations Of Graphs More PreCalculus Lessons Common Core (Functions) We shall learn how to identify the effect on the graph of replacing f(x) by f(x) k, kf(x), f(kx), and f(x k) for specific values of k (both positive and negative);
Geometric Transformations of Functions We start with a java applet to explore graphically the basic geometric transformations of functions We now proceed to express these geometrical transformations in algebraic terms Translations of Functions Suppose that y = f (x) is a function and c > 0;New Resources Keishiro Ueki 31 okt ; Transformation How do the graphs of y = f (x) k, y = f(x – h), and y = f(x) compare to the graph of the parent function f?



Graph Transformations Y F X K Geogebra




Stretching And Reflecting Transformations Read Algebra Ck 12 Foundation
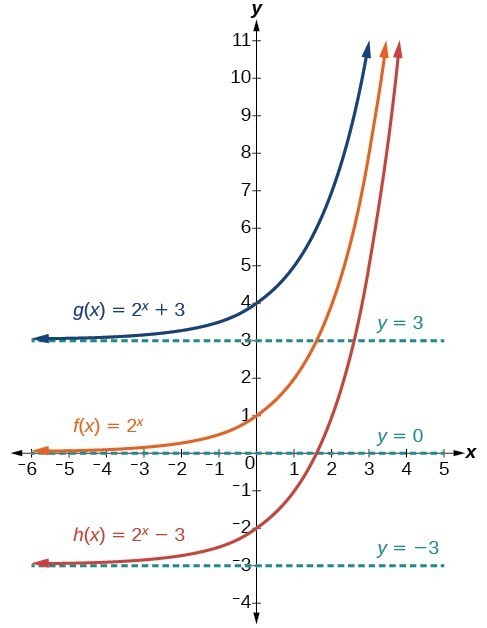
If 3 so, describe at least one other possible sequence of transformationsTransformations of exponential graphs behave similarly to those of other functions Just as with other parent functions, we can apply the four types of transformations—shifts, reflections, stretches, and compressions—to the parent function latexf\left(x\right)={b}^{x}/latex without lossIn two ways f(x 1) f ( x 1) is a change on the inside of the function, giving a horizontal shift left by 1, and the subtraction by 3 in f(x 1) − 3 f ( x 1) − 3 is a change to the outside of the function, giving a vertical shift down by 3 The transformation of the graph is illustrated below



Transformations



Graph Transformations 2 Fx A Copy Youtube
Since it says plus and the vertical changes act the way they look, the actual translation is to move the entire graph two units up or "add two to every ycoordinate" while leaving the xcoordinates alone y=f (x3)5 This time, there is a horizontal shiftPrecalculus (2nd Edition) Edit edition Solutions for Chapter 17 Problem 6E Match the rigid transformation of y = f(x) with the correct representation of the graph of h, where c > 0 Solutions for problems in chapter 17 Mr Jeffery demonstrating an easy trick that will allow you to work out graph transformation questions using a simple to follow method



Transformation Of Graphs Starting At Y F X Simple Pt 2 Youtube




How To Graph Transformations Of Functions 14 Steps
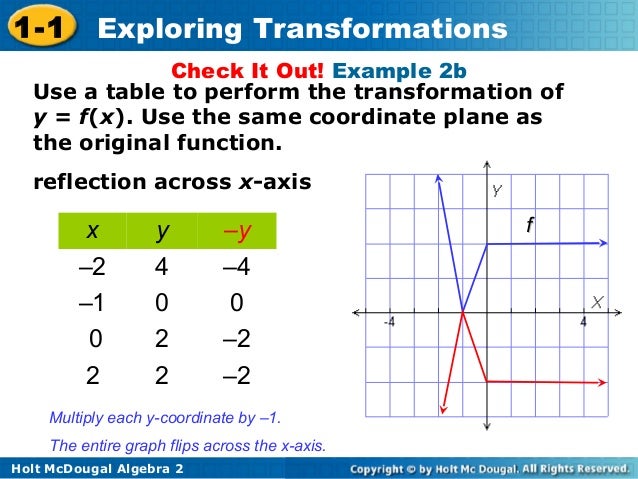
The graph of y = f (x) is transformed into y = – f ((x 9)) 8 a Describe the transformations in the correct order b Is it possible that another sequence of transformations could produce the same graph as y = – f ( (x 9)) 8?Y = f (x) becomes y = f (x ± a) These transformations are called horizontal shifts or translations They move the graph of the given function left (adding positive a) or right (subtracting positive a) The parameter a can multiply the input x before the rule f is appliedPurplemath There are two other transformations, but they're harder to "see" with any degree of accuracy The first of these transformation is multiplication on the entire function To see what this looks like, compare the graphs of 2 × f (x) = 2x2, f (x) = x2, and ½ × f (x) = (½) x2, below graph of 2 × f (x) = 2x2 (This is skinnier




Lesson Explainer Function Transformations Translations Nagwa




Transforming Graphs Of Functions Brilliant Math Science Wiki
View my channel http//wwwyoutubecom/jayates79Let us start with a function, in this case it is f(x) = x 2, but it could be anything f(x) = x 2 Here are some simple things we can do to move or scale it on the graph We can move it up or down by adding a constant to the yvalue g(x) = x 2 C Note to move the line down, we use a negative value for C C > 0 moves it up;Graph transformation is the process by which an existing graph, or graphed equation, is modified to produce a variation of the proceeding graph It's a common type of problem in algebra, specifically the modification of algebraic equations Sometimes graphs are translated, or moved about the x y
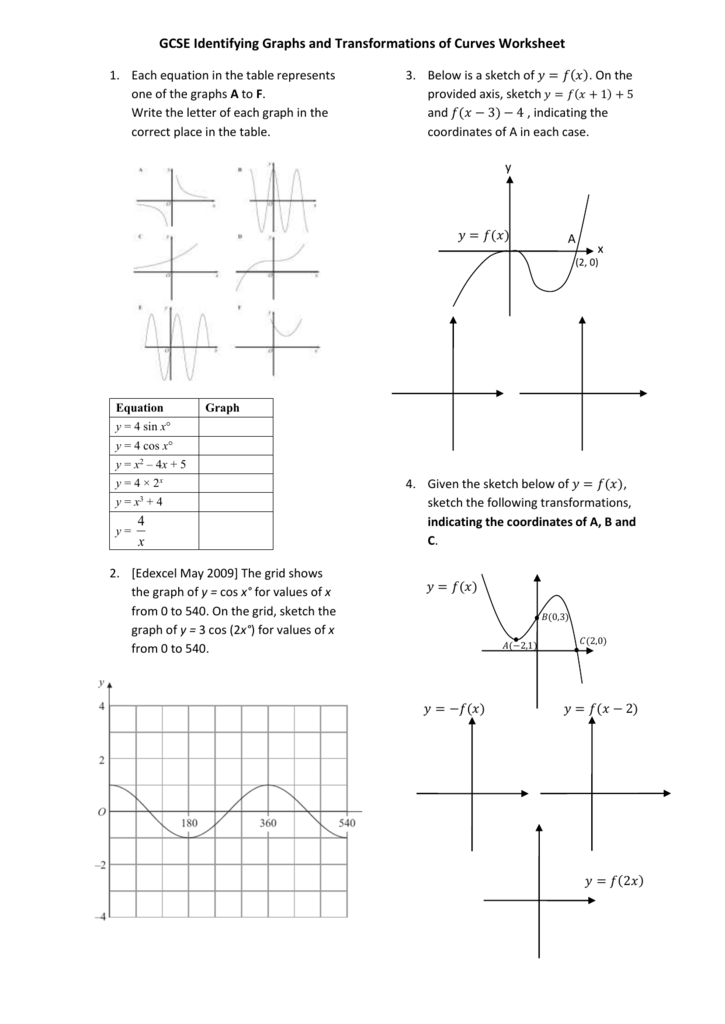



Gcse Transformations Of Curves Worksheet



Transformations Mrs F X
Question 5 Compare the graph of each function to the graph of its parent function f Use a graphing calculator to verify your answers are correctThe graph of y= Af B(xh) kis a transformation of the graph of y= f(x) The transformations can be done in the following order • A The function stretches or compresses vertically by a factor of A If A is negative, the function also reflects across the xaxis ZioX You take the graph of f (x) and shift it down four units (Assuming fR>R) I think ZioX is right From what I remember, f (x) is the same thing as y so it's saying (IMO) y = 4 So it would be shifted down 4 units and you should have a horizontal line You take the graph of f (x) and shift it down four units



Graphing With Transformations Quantitative Reasoning
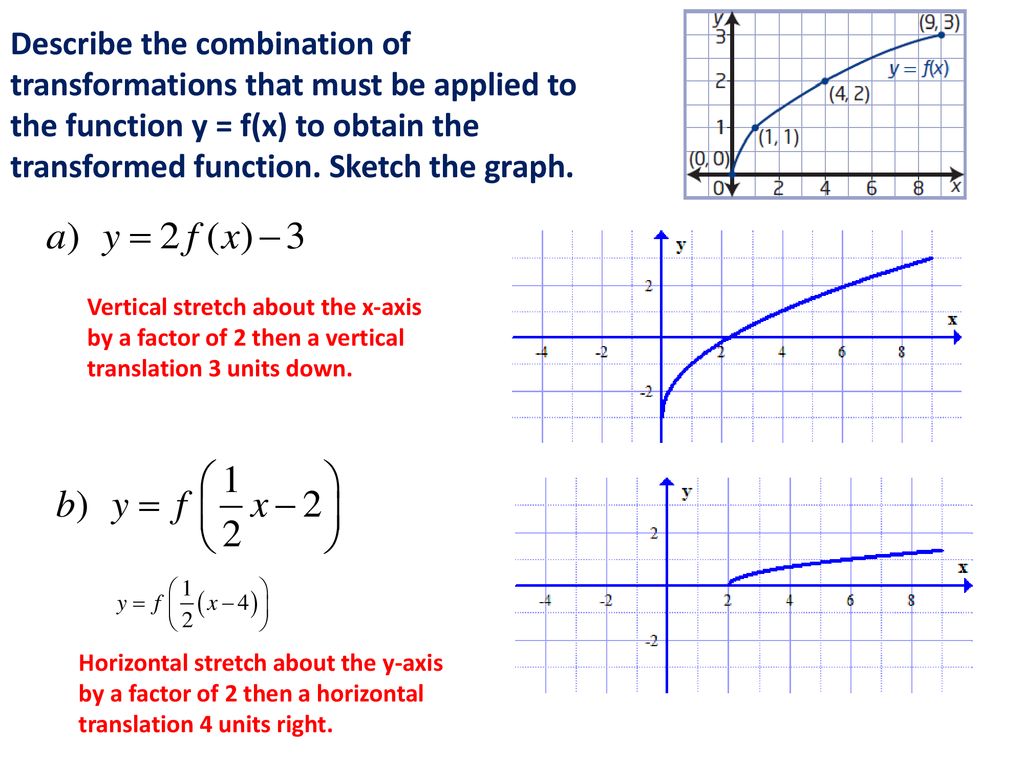



1 3 Combining Transformations Ppt Download
Graph of a function being reflected The function latexf(x)=x^5/latex is reflected over the latexy/latexaxis Rotations A rotation is a transformation that is performed by "spinning" the object around a fixed point known as the center of rotationMathematics Stack Exchange is a question and answer site for people studying math at any level and professionals in related fields It only takes a minute to sign up 6 Determine the left/right flip The left/right flip determines if the graph will flip over the yaxis This flip means the original graph will be flipped the opposite direction across the yaxis, either to left or right If the variable of the function is multiplied by




Horizontal And Vertical Graph Transformations Examples Solutions Videos Worksheets Games Activities



Q Tbn And9gcqhc H7dg7yh3yw9myrx S Xshwo3q3m8cp73od Ad5nw X4evk Usqp Cau
The graph of y=f(x) is a transformation of the graph y=g(x) Write a formula for function f in terms of function g Answers 1 Show answers Another question on Mathematics Mathematics, 1800 What is the standard deviation of 1, 221, 180,Section 56 Graphical Transformations In this section we are going to explore the graphical repercussions of alterations to a given function formula Specifically, we are going to explore how the graph of the function \(g\) compares to the graph \(f\) where 1 You are correct, given any function f ( x), you get the graph of f ( x ) by taking the graph of f, deleting the graph where x < 0, then reflecting the graph where x > 0 into the region you deleted To understand the answer described in your second paragraph, think of f ( x − 1 ) as g ( x − 1) where we define g as the new function g



1 5 Shifting Reflecting And Stretching Graphs



Function Transformations
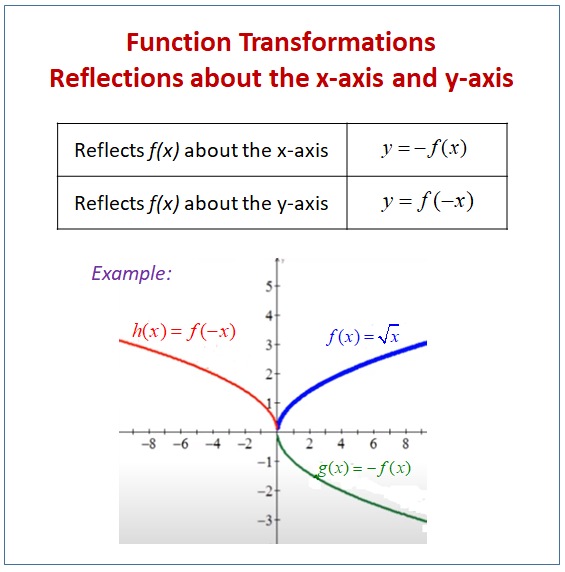
Example 2 Write the steps to obtain the graph of the function y = 3 (x − 1) 2 5 from the graph y = x 2 Solution Step 1 By graphing the curve y = x 2, we get a open upward parabola with vertex (0, 0) Step 2 Here 1 is subtracted from x, so we have to shift the graph of y = xAbsolute Value and Distance;The last two easy transformations involve flipping functions upside down (flipping them around the x axis), and mirroring them in the y axis The first, flipping upside down, is found by taking the negative of the original function;
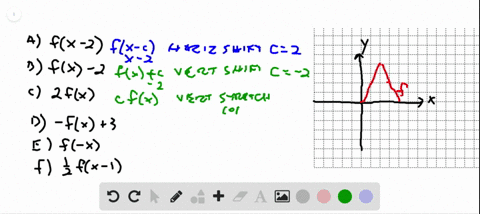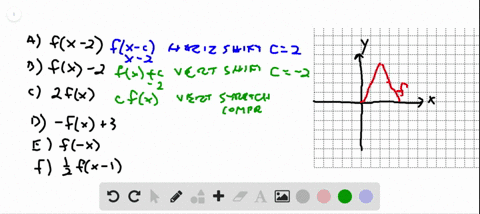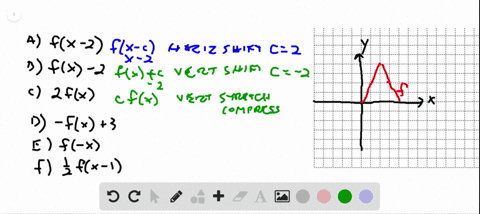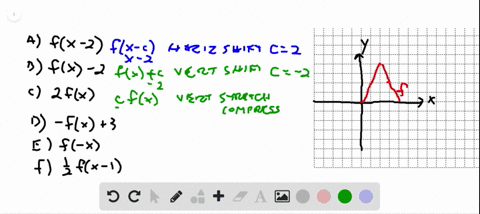



Solved 69 70 Identifying Transformations The Graph Of Y F X Is Given Match Each Equation With Its Graph Begin Arra




Transformations Similarity
Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!C < 0 moves it down 17 Transformations In this section, we study how the graphs of functions change, or transform, when certain specialized modifications are made to their formulas The transformations we will study fall into three broad categories shifts, reflections and scalings, and we will present them in that order



Question Video Transformations Of Graphs Nagwa




Transformation Of Graphs Maths Numeracy Educational School Posters
Combining Vertical and Horizontal Shifts Now that we have two transformations, we can combine them together Vertical shifts are outside changes that affect the output ( yy) axis values and shift the function up or downHorizontal shifts are inside changes that affect the input ( xx) axis values and shift the function left or rightCombining the two types of shifts will cause the graph ofFunctions of graphs can be transformed to show shifts and reflections Graphic designers and 3D modellers use transformations of graphs to design objects and imagesFunctions & Graphing Calculator \square!




Algebra Graph Transformations Examsolutions



Reflecting Functions Or Graphs Examples Solutions Worksheets Videos Games Activities
Transformations of Graphs Suppose we know what the graph of y f x looks like If c 0, then we can determine the graph that results when we define some new functions in terms of c, x, and f x Type of Transformation To Graph Do this to the graph of y f xGraph Transformations There are many times when you'll know very well what the graph of a particular function looks like, and you'll want to know what the graph of a • Beginning with the graph f(x)=x2, we can use the chart on the previous page to draw the graphs of f(x 2),f(x 2), f(2x), f(1 2x), and f(x)Geometry of 2x2 Matrix Multiplication with Intro Questions;



1 7a 1 Mathpower Tm 12 Western Edition Chapter 1 Transformations 1 7a Ppt Download



Transformations Of Functions Mathbitsnotebook A1 Ccss Math
The graphs of y = √x, g(x), and h(x) are shown below Describe the transformations done on each function and find their algebraic expressions as well The function h(x) can be attained by translating y = x 3 by 2 units to the left and 4 units upwardThe simplest shift is a vertical shift, moving the graph up or down, because this transformation involves adding a positive or negative constant to the function In other words, we add the same constant to the output value of the function regardless of the input For a function g(x) = f(x) k g ( x) = f ( xAnother fantastic video from wwwMathsMasterOrg



The Graph Of Y F X Is Shown Sketch The Graph Of Y Chegg Com




Graph Transformations Of Y F X Easy Trick Gcse Edexcel Maths 9 1 Youtube
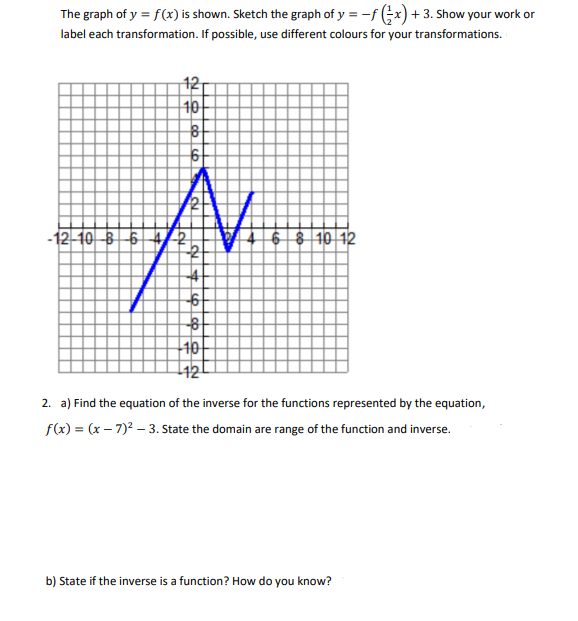
Precalculus questions and answers The graph of a function f is given Sketch the graphs of the following transformations of f (b) y = f (x) − 3 (c) y = 2f (x) (d) y = −f (x) 5 (e) y = f (−x) (f) y =1/2f (x − 4) Question The graph of a function f is given Sketch the graphs of the following transformations of f y=f (x) will indicate that the graph has reflected about the yaxis y=f (x) will indicate that the graph has reflected about the origin If I have f (x)= (x) 3, then the graph would be reflected about the yaxis Try to experiment on these transformations by using a graphing utility such as Desmos, Symbolab, GeoGebraGraphing Transformations of Logarithmic Functions As we mentioned in the beginning of the section, transformations of logarithmic graphs behave similarly to those of other parent functions We can shift, stretch, compress, and reflect the parent function y = l o g b ( x) \displaystyle y= {\mathrm {log}}_ {b}\left (x\right) y = log




Solution Order Order Combining Functions Underground Mathematics




The Graph Shown Is A Transformation Of The Parent Function F X X Choose The Equation Which Represents The Transformation Shown Study Com
17 Transformations 123 2 to all of the xvalues of the points on the graph of y= f(x) to e ect a shift to the right 2 units Generalizing these notions produces the following resultGiven y=f(x), how do you graph y=f(1/x)?That is, the rule for this transformation is –f (x)




Function Transformations




A Given The Graph Of F X Below Graph The Chegg Com
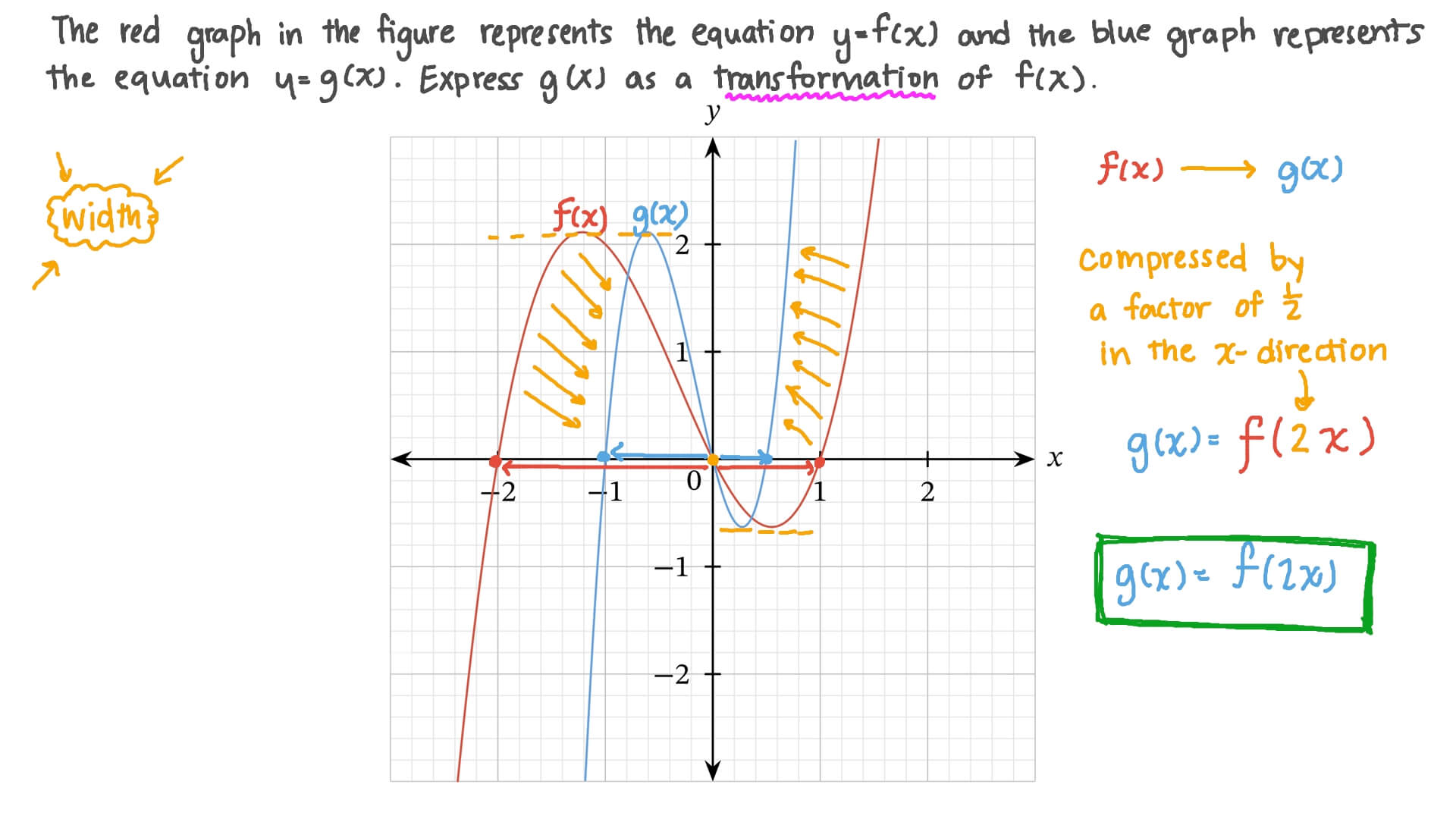
Find the value of k given the graphsIs a rigid transformation that shifts a graph up or down relative to the original graph This occurs when a constant is added to any function If we add a positive constant to each y coordinate, the graph will shift up If we add a negative constant, the graph will shift downSo this red curve is the graph of f of X and this blue curve is the graph of G of X and I want to try to express G of X in terms of f of X and so let's see how they're related so we pick any X and we could start right here at the vertex of f of X and we see that at least at that point G of X is exactly one higher than that so G of two I could write this down G of two G of two is equal to is




Combining Transformations Read Algebra Ck 12 Foundation
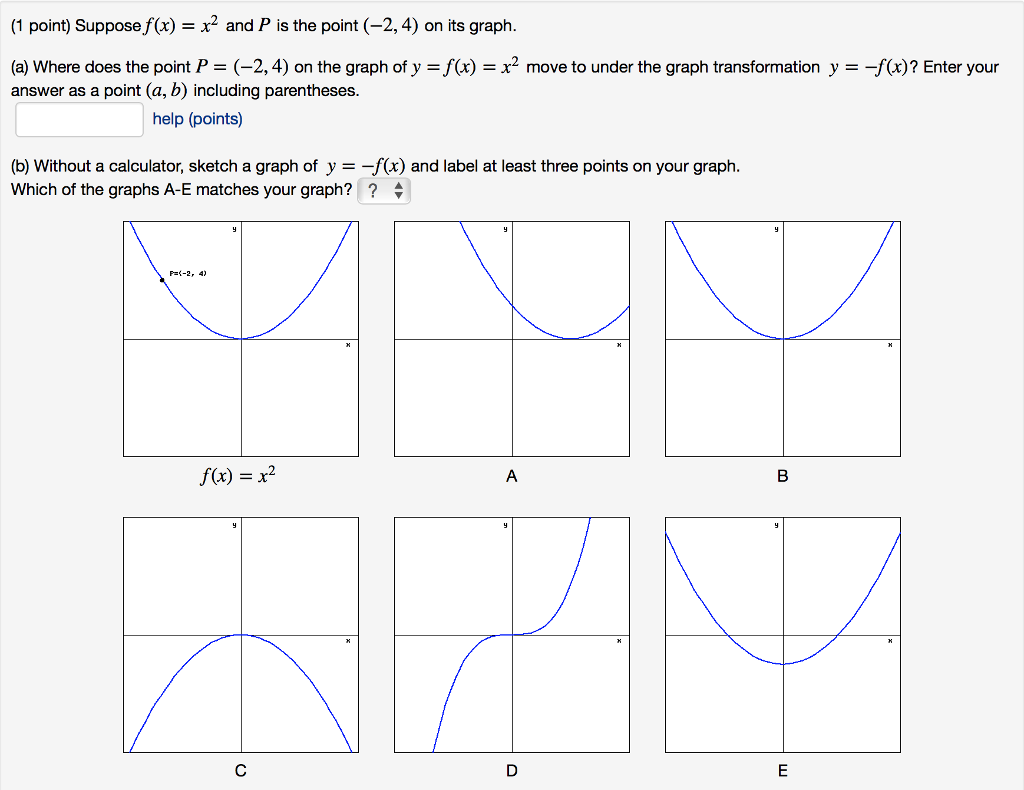



Suppose F X X 2 And P Is The Point 2 4 On Its Chegg Com
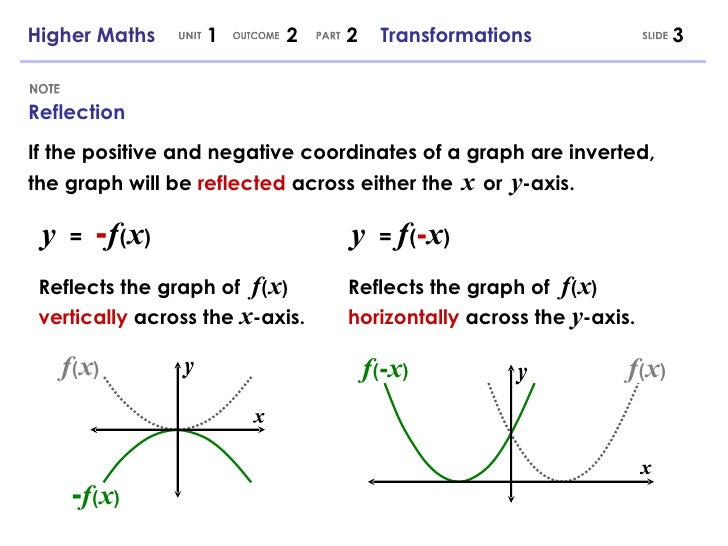



Higher Maths 1 2 2 Graphs And Transformations



Transformation Of Graph L2 Modulus Function Graphs Of Y F X Y F X Y F X With Examples Youtube



Transformations Of Graphs 2 Y F Ax Geogebra
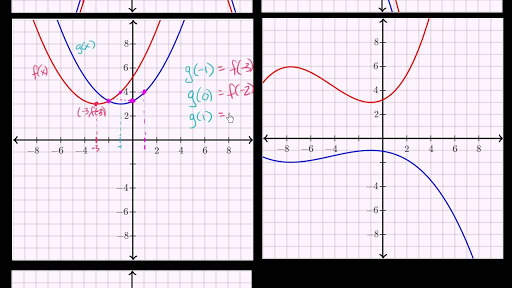



Identifying Function Transformations Video Khan Academy



The Graph Of Y H X Is A Transformation Of The Graph Of Y G X Steps Please Thank You Socratic



Transformations Of Functions Mathbitsnotebook A1 Ccss Math
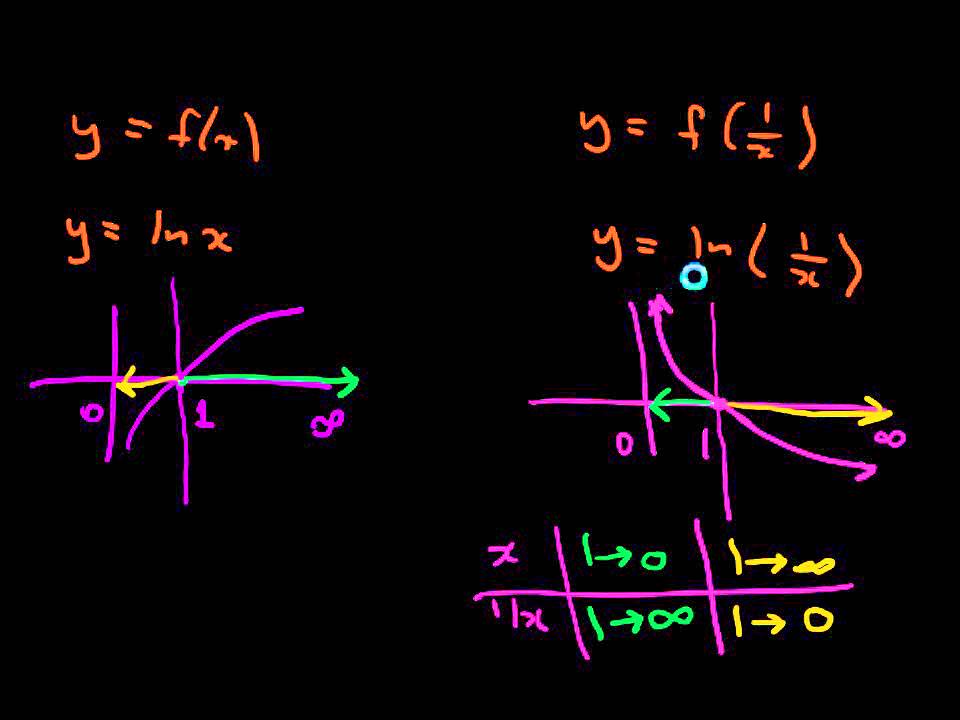



Graphing Transformation Y F 1 X Youtube
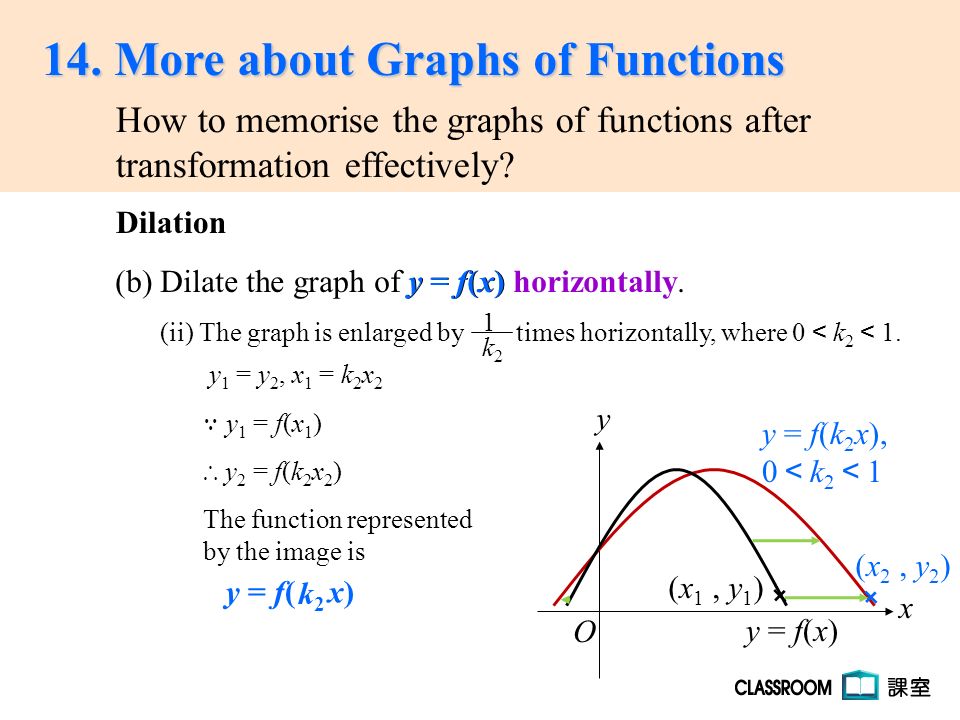



14 More About Graphs Of Functions Transformation Effectively How To Memorise The Graphs Of Functions After O Y X A Translate The Graph Of Y F X K Ppt Download




Transformations Of Graphs Trevor Pythagoras




Interpret The Graph Of Frac Ax B Cx D As A Transformation Of Y Frac 1 X Mathematics Stack Exchange



Transformations Of Functions Mathbitsnotebook A1 Ccss Math
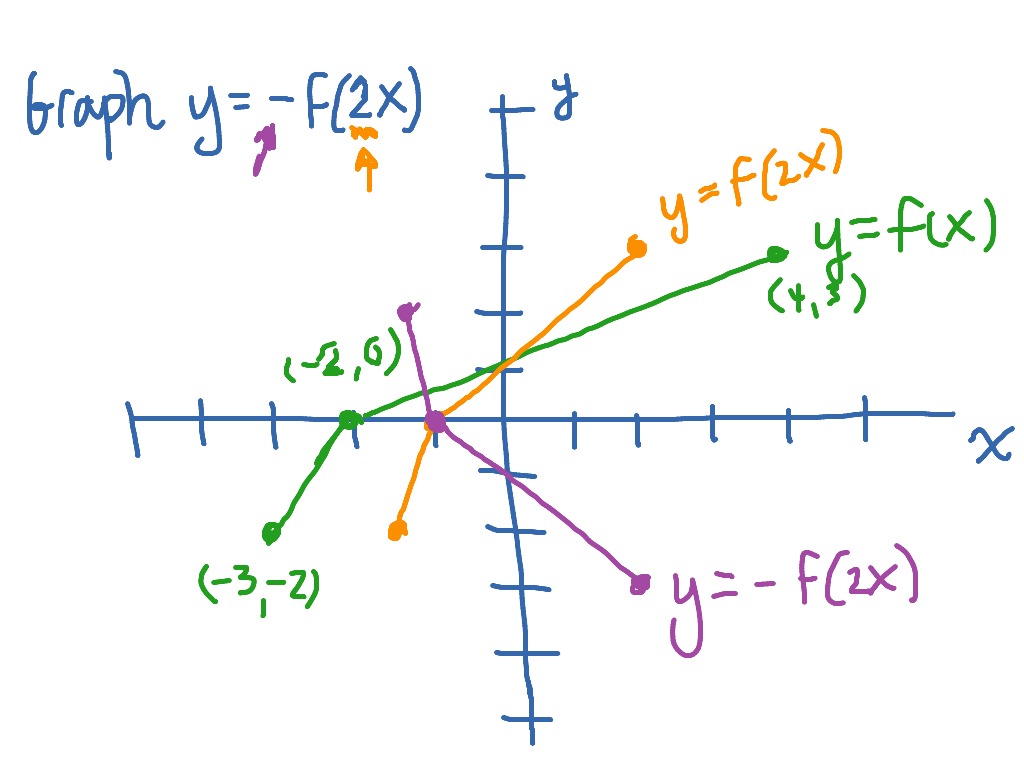



Graphing Y F 2x As A Transformation Of Y F X Math Showme



Shifting Of Graphs Transformation Example 1 Y F X Kup K Units Y F X Kdown K Units Vertical Shifting Below Is The Graph Of A Function Y Ppt Download



Function Transformations



Transformations Of Functions Mathbitsnotebook A1 Ccss Math




Graph Transformations With Examples Gcse Mitch Maths




Simple Graph Transformation Question Rightarrow 1 F X Mathematics Stack Exchange



Solution How Do These Transformations Change The Graph Of F X Combining Functions Underground Mathematics



Graph Transformations Y F X K Geogebra
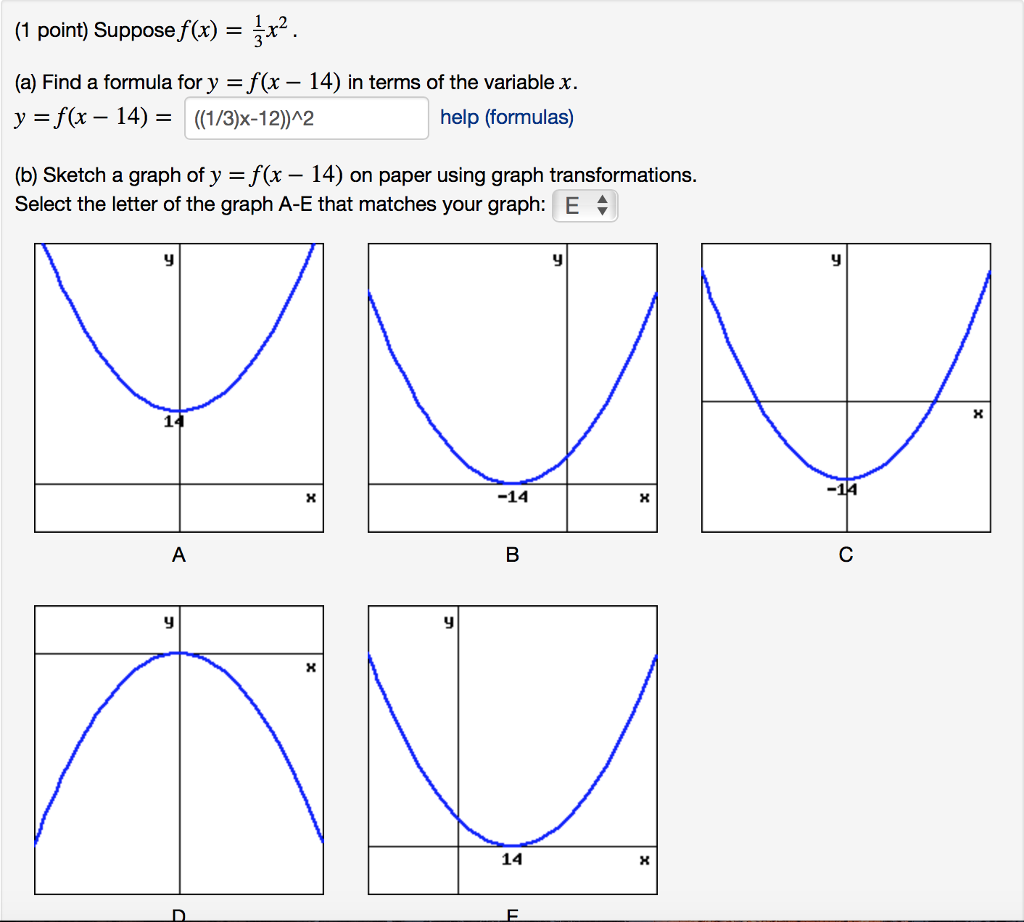



Suppose F X 1 3 X 2 A Find A Formula For Y Chegg Com
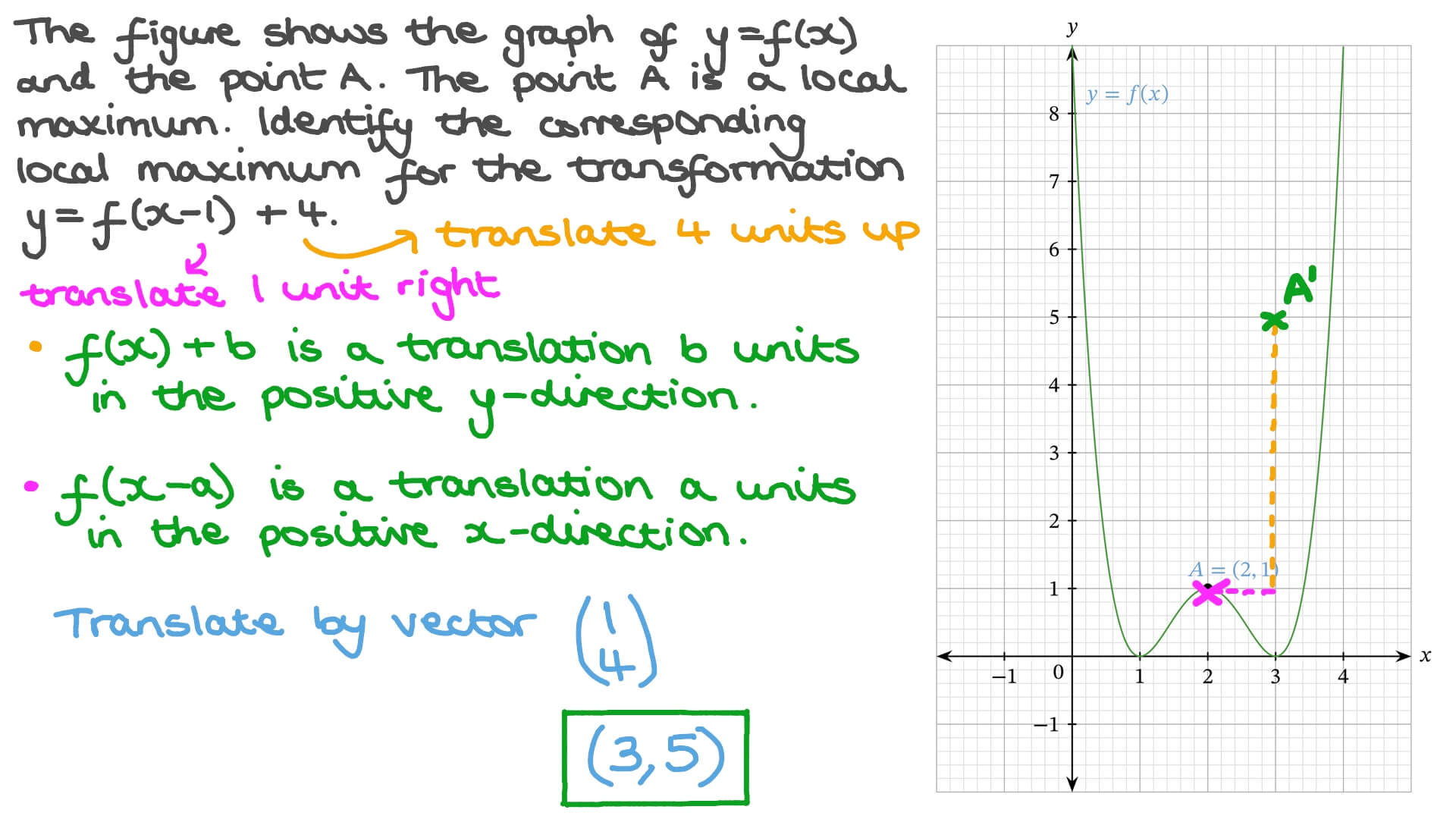



Question Video Identifying The Coordinates Of Points Following A Transformation Nagwa



Transformations Of Functions Mathbitsnotebook A1 Ccss Math



1




Geogebra In The Classroom Single Graph Transformations




The Graph Of F Is Given By Draw The Graphs Of The Following Functions A Y F X 3 B Y F X 1 C Y Frac 1 2 F X D Y F X Study Com



3 5 Transformations Of Functions 2 5 Ncb 502 Corequisite For Mat 1023 Openstax Cnx
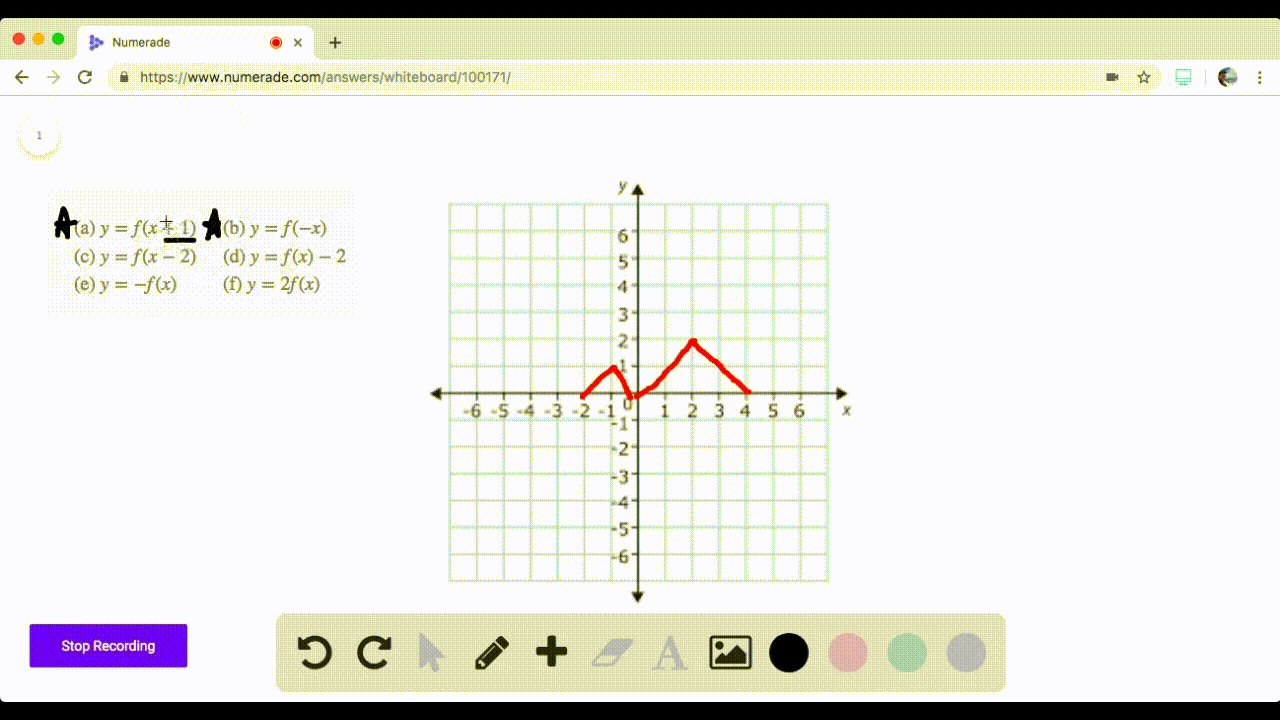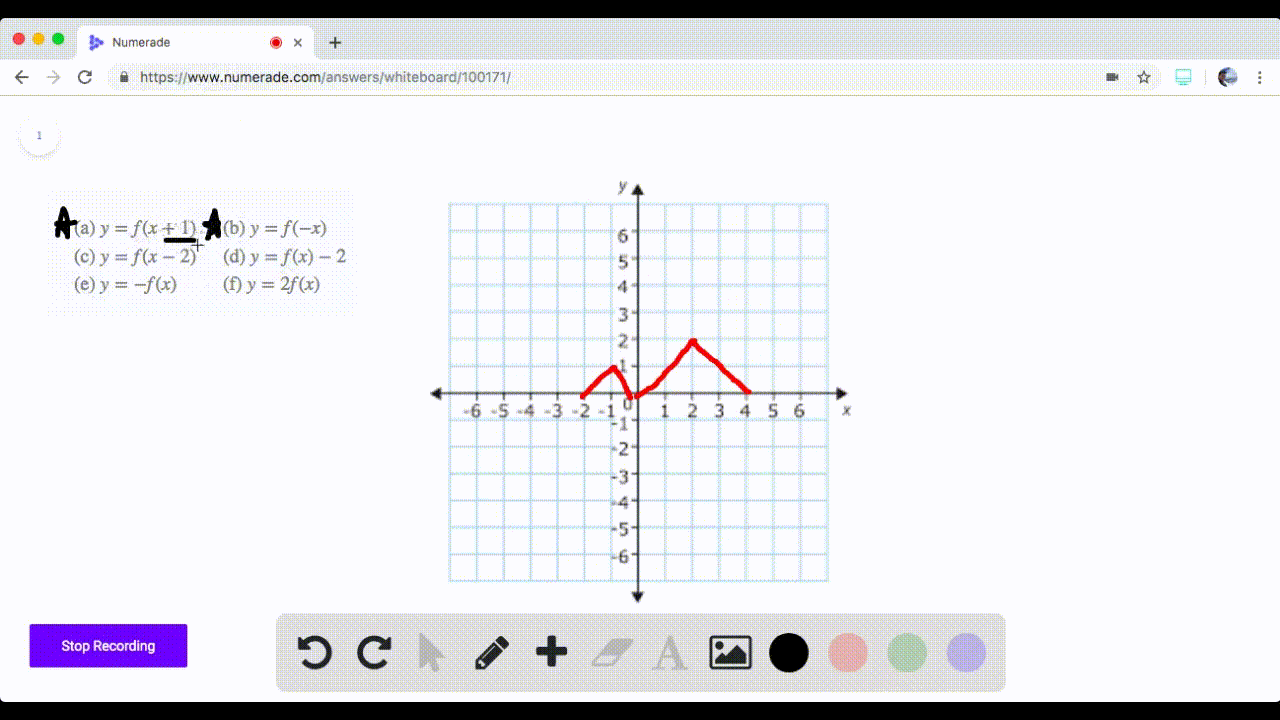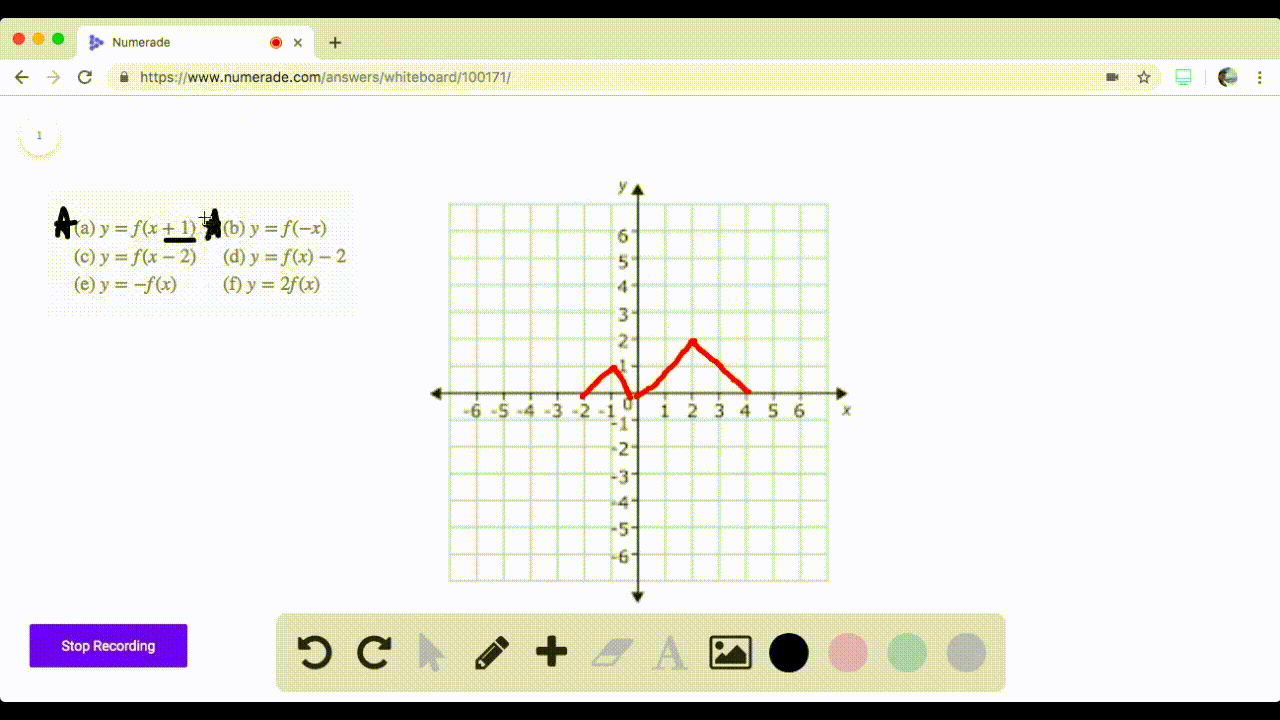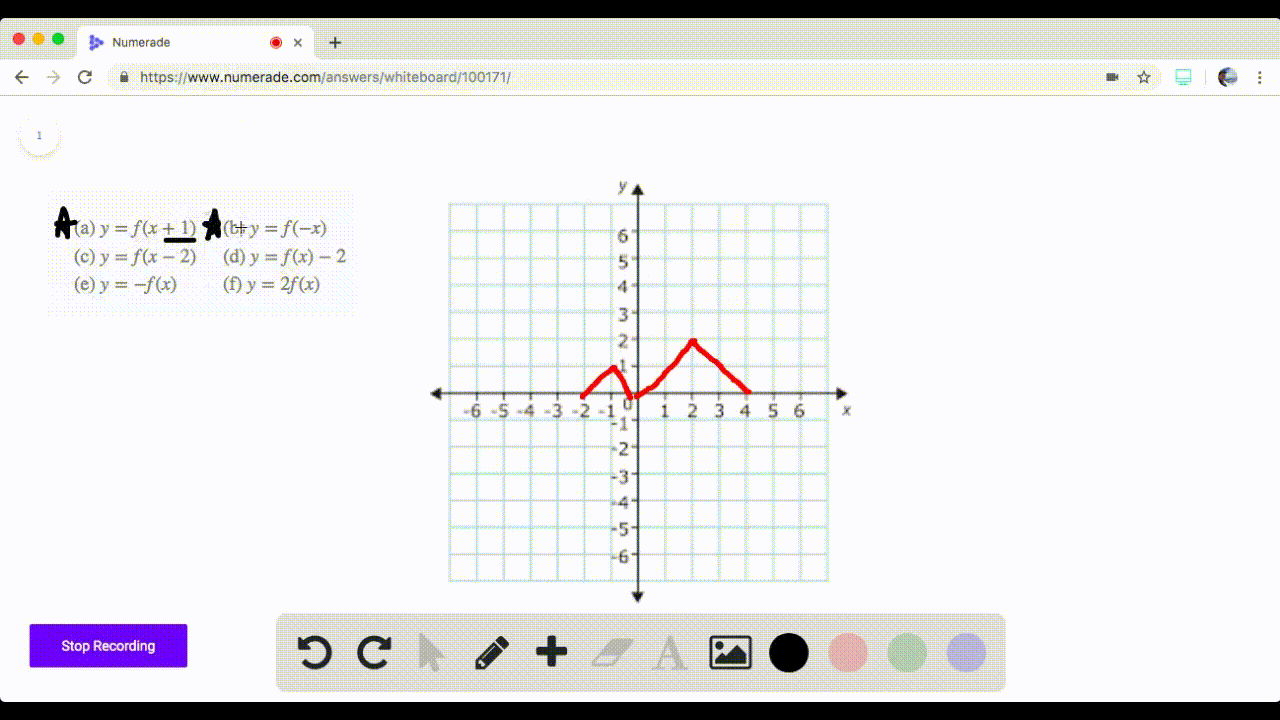



Solved 71 74 Graphing Transformations The Graph Of A Function F Is Given Sketch The Graphs Of The Following Transform




Using Transformations To Graph Functions
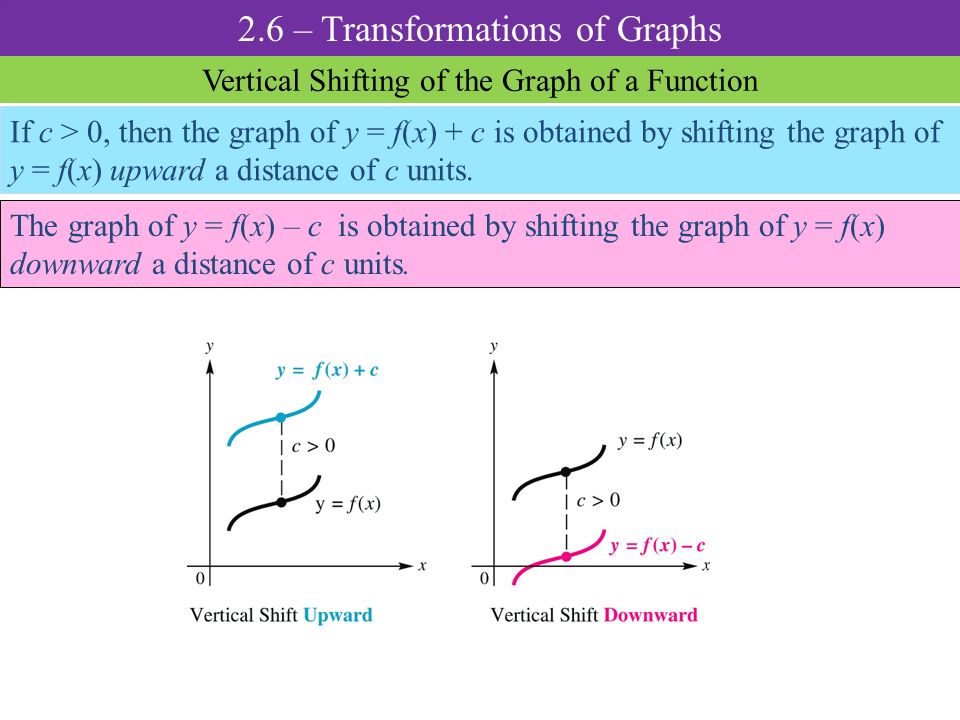



2 6 Transformations Of Graphs Ppt Download



Transformations




College Algebra Chapter 2 Functions And Graphs Section



Body




Transformations Of Graphs Reflections Y F X Y F X Proof Examsolutions Youtube




Transforming Graphs Of Functions Ppt Download



Biomath Transformation Of Graphs




Ppt Graph Transformations Powerpoint Presentation Free Download Id



3 5 Transformations Of Graphs Graph Functions Using



1 1



Graph Transformations In Zoom




Graph Transformations With Examples Gcse Mitch Maths



Graph Transformations Y F X A Geogebra




Transformations Of Functions Mathematics Learning And Technology



Transformations Of Graphs Reflections Y F X F X Examsolutions Youtube




3 5 Transformations Of Graphs Graph Functions Using




Transformations
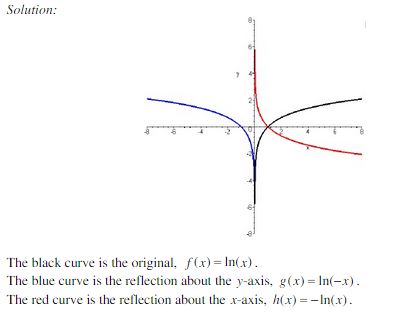



Transformation Of Exponential And Logarithmic Functions Nool
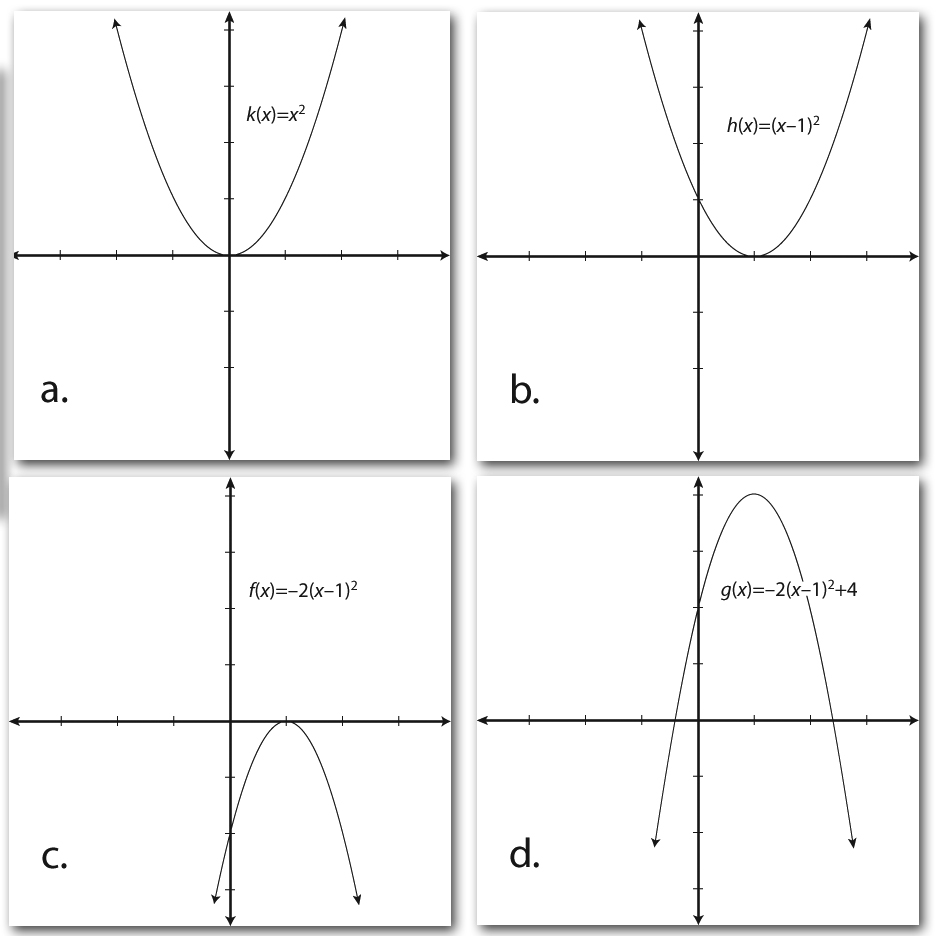



How To Combine Various Transformations Dummies
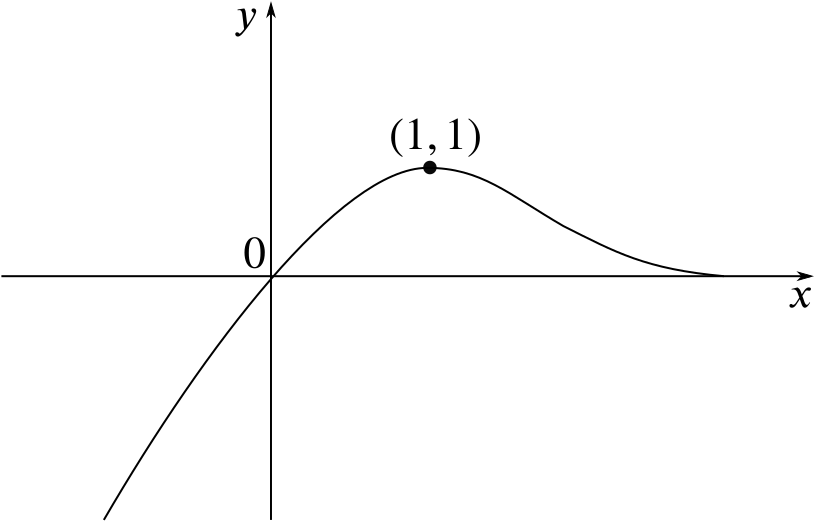



Solution How Do These Transformations Change The Graph Of F X Combining Functions Underground Mathematics



3 5 Transformations Of Graphs Graph Functions Using




Transforming Graphs Of Functions Brilliant Math Science Wiki



Graph Exponential Functions Using Transformations College Algebra




Graph Transformations With Examples Gcse Mitch Maths




Transformation Of Graphs I Definition Examples Diagrams



Solution How Do These Transformations Change The Graph Of F X Combining Functions Underground Mathematics
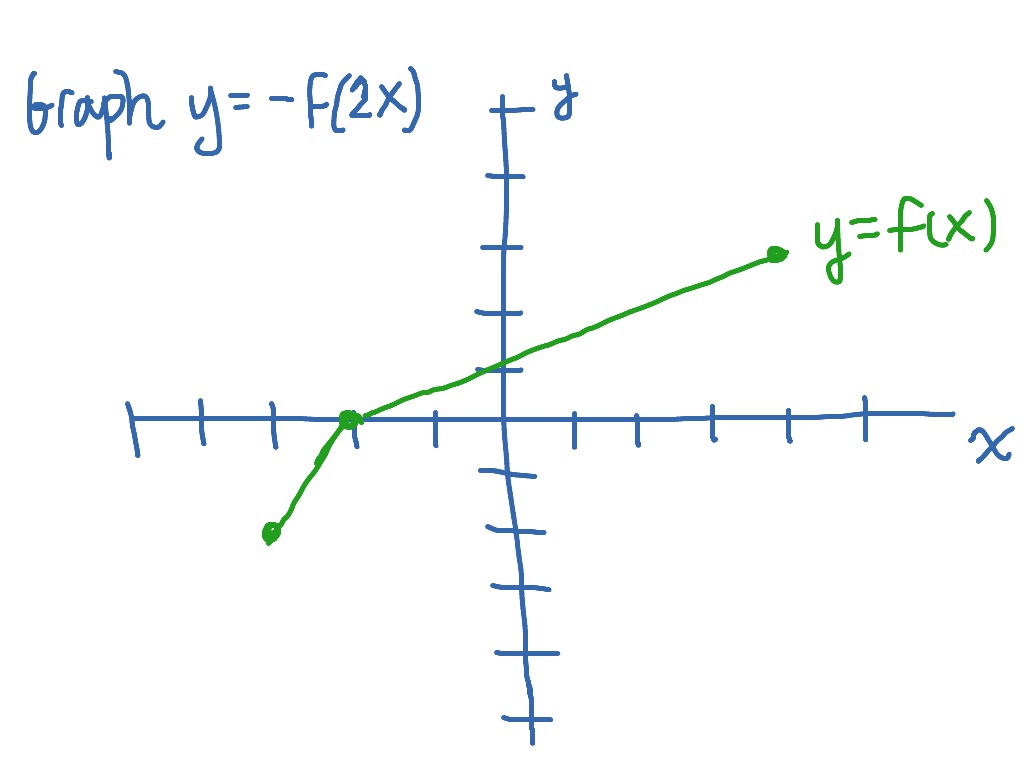



Graphing Y F 2x As A Transformation Of Y F X Math Showme
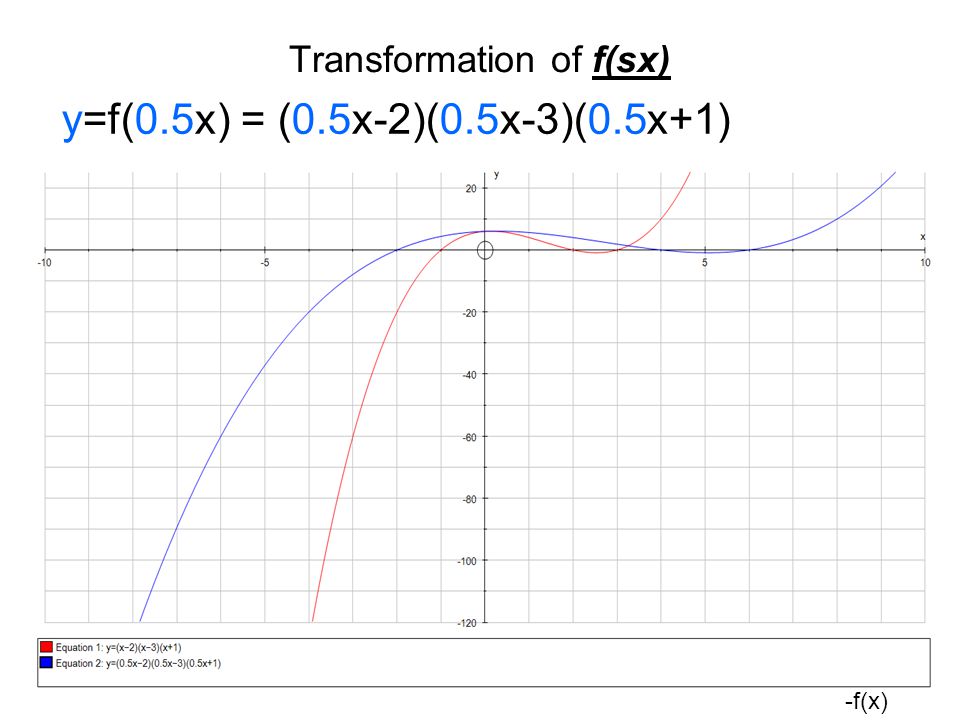



Transformation Of Graphs Andrew Robertson Transformation Of F X A F X X Ppt Download



Graphical Transformation Functions F X Wethestudy



Graph Transformations



3 5 Transformations Of Graphs Graph Functions Using




Transformations Of Functions Mathematics Learning And Technology




Graph Transformation Y F X A Of The Function F X Youtube




Transformations Mathematics Learning And Technology




The Limit Of A Function Utrgv



Q Tbn And9gcsl0jyluxfxjjcizs7jyiyflsxbm6hpbpzdawckl4kjhmo0pmir Usqp Cau
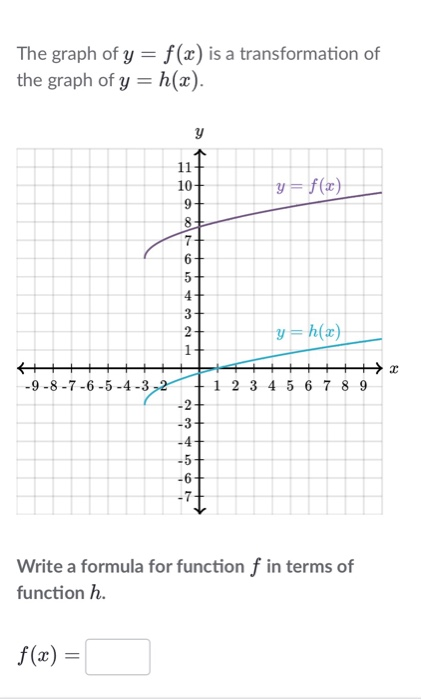



The Graph Of Y F X Is A Transformation Of The Chegg Com



The Graph Of The F X Is Show Below Graph Each Transformed Function And List In Words The Transformation Used Socratic



Transformations Of Functions Mathbitsnotebook A1 Ccss Math
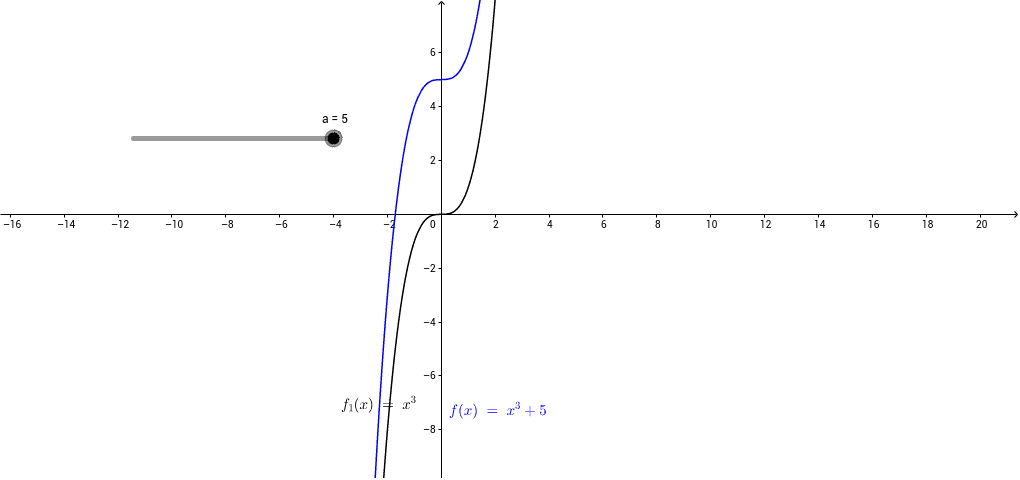



Graph Transformations Y F X A Geogebra




Exam Questions Graph Transformations Examsolutions
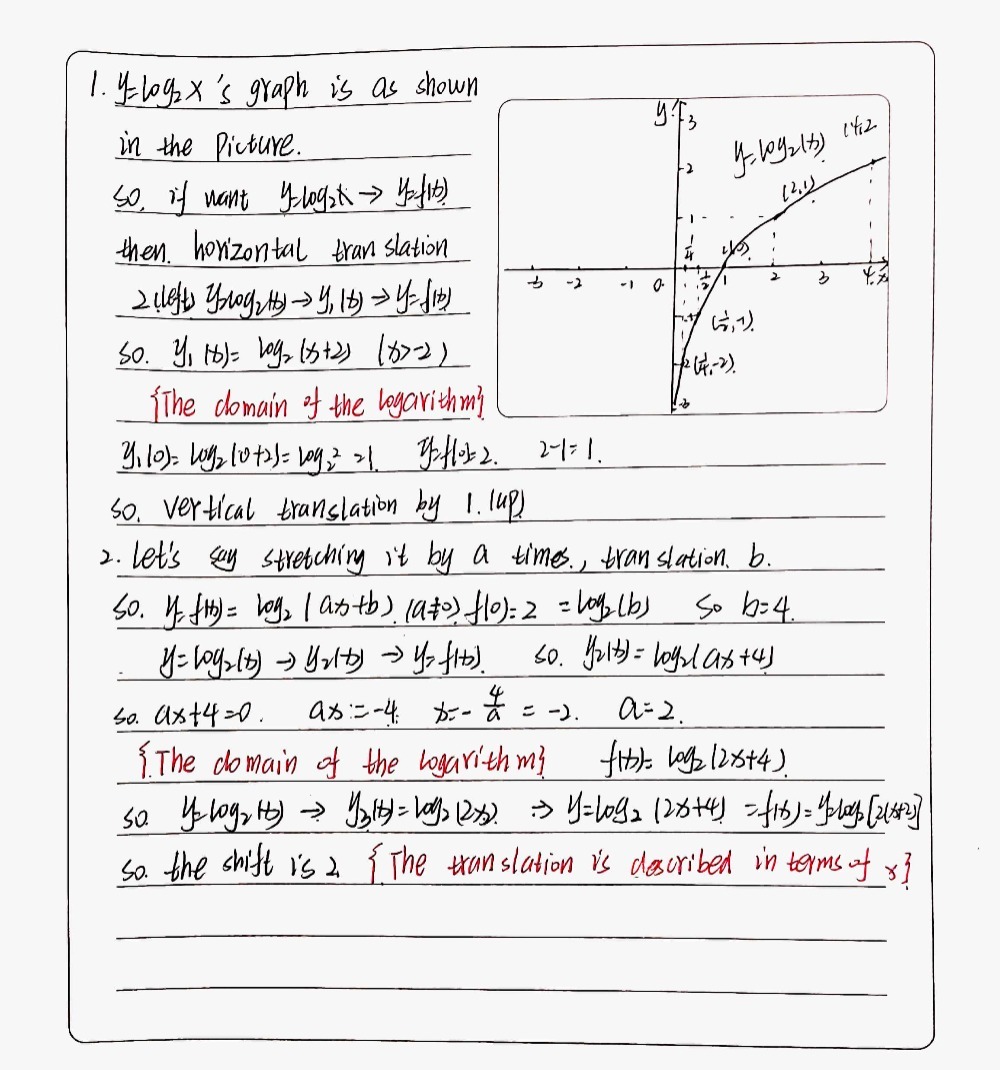



Part 1 The Graph Of Fx Is Shown It Goes Through Gauthmath




Transformations Of Graphs Af X F Ax F X F X F X A F X A Teaching Resources



1



0 件のコメント:
コメントを投稿